Ingeniería Civil
Unidad de Aprendizaje: Métodos Numéricos
Grupo: 401 Turno: Matutino
Maestra: Lorena Alonso Guzmán
Mario Sigifredo López Romero
Índice
1.-Introducción
2.-Definición de métodos numéricos
2.1.- Aproximación y errores
2.2.- Exactitud
2.3.-Precisión
2.4.- Incertidumbre
2.4.1.- Sesgo
2.5.-Errores humanos
2.6.- Serie de Taylor
3-. Conceptos básicos
3.1.- Algoritmos
3.2.- Aproximaciones
4.- Tipos de errores
4.1.- Error absoluto
4.2.- Error relativo
4.3.- Error porcentual
4.4.- Errores de redondeo
4.5.- Error de truncamiento
5.- convergencia
6.- programas computacionales
7.- conclusión
8.- bibliografía
1.- Introducción
Al momento de aplicar las Matemáticas a situaciones del mundo real nos encontramos a menudo con problemas que no pueden ser resueltos
analíticamente o de manera exacta y cuya solución debe ser abordada con ayuda de algún procedimiento o método numérico.
El objetivo principal del análisis numérico es encontrar soluciones “aproximadas” a problemas complejos utilizando sólo las operaciones más simples de la aritmética. Se requiere de una secuencia de operaciones algebraicas y lógicas que producen la aproximación al problema matemático.
El análisis numérico trata de diseñar métodos para “ aproximar” de una manera eficiente las soluciones de problemas expresados matemáticamente.
2.- Definición de Métodos Numéricos
Los métodos numéricos no son más que procedimientos a seguir para la resolución u obtención aproximada, de problemas matemáticos, realizando cálculos aritméticos y lógicos como operaciones aritméticas elementales, consulta de tablas de valores, cálculo de funciones, etc.
Un tal procedimiento consiste de una lista finita de instrucciones precisas que especifican una secuencia de operaciones algebraicas y lógicas (algoritmo), que producen o bien una aproximación de la solución del problema (solución numérica) o bien un mensaje. La eficiencia en el cálculo de dicha aproximación depende, en parte, de la facilidad de implementación del algoritmo y de las características especiales y limitaciones de los instrumentos de cálculo (los computadores).
2.1.- Aproximación y Errores
Aproximación
Se entiende por aproximación, una cifra que representa un número cuyo valor exacto es X. En la medida en que la cifra X se acerca más al valor exacto X, será una mejor aproximación de ese número.
3.1416 es una aproximación numérica de Pi (π).
2.7183 es una aproximación numérica de e.
0.333333 es una aproximación numérica de 1/3.
Errores
El error podemos definirlo como la discrepancia entre la magnitud “verdadera” y la obtenida, siendo dichas magnitudes los resultados de la medición.
2.2.- Exactitud
Se refiere a la aproximación de un número o de una medida al al valor numérico que se supone representa.
2.3.- Precisión
se refiere a la dispersión del conjunto de valores obtenidos de mediciones repetidas de una magnitud. Cuanto menor es la dispersión mayor la precisión. Una medida común de la variabilidad es la desviación estándar de las mediciones y la precisión se puede estimar como una función de ella.
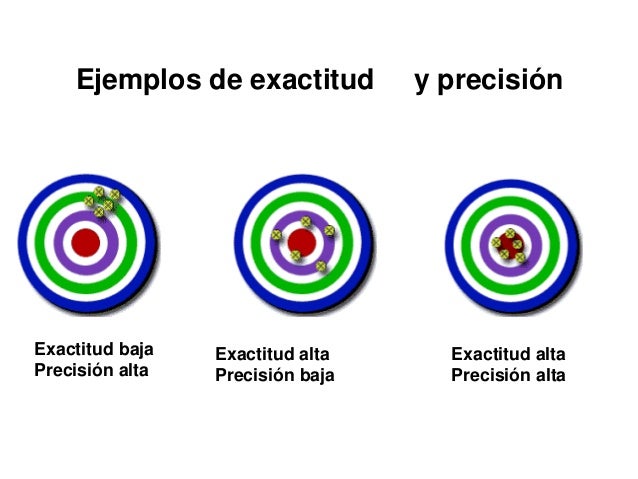
Incertidumbre también se le conoce como Imprecisión. Se refiere al grado de alejamiento entre sí, a las diversas aproximaciones a un valor verdadero.
Situación bajo la cual se desconocen las probabilidades de ocurrencia asociados a los diferentes resultados de un determinado evento.
2.4.1.- Sesgo
Existe sesgo cuando la ocurrencia de un error no aparece como un hecho aleatorio (al azar) advirtiéndose que este ocurre en forma sistemática
2.5.- Errores Humanos
Son los errores por negligencia o equivocación. Las computadoras pueden dar números erróneos por su funcionamiento. Actualmente las computadoras son muy exactas y el error es atribuido a los hombres. Se pueden evitar con un buen conocimiento de los principios fundamentales y con la posesión de métodos y el diseño de la solución del problema. Los errores humanos por negligencia son prácticamente inevitables pero se pueden minimizar.
Una serie de Taylor es una aproximación de funciones mediante una serie de potencias o suma de potencias enteras de polinomios como
llamados términos de la serie, dicha suma se calcula a partir de las derivadas de la función para un determinado valor o punto 
suficientemente derivable sobre la función y un entorno sobre el cual converja la serie. Si esta serie está centrada sobre el punto cero,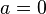 
, se le denomina serie de McLaurin.Esta aproximación tiene tres ventajas importantes:
- la derivación e integración de una de estas series se puede realizar término a término, que resultan operaciones triviales;
- se puede utilizar para calcular valores aproximados de funciones;
- es posible calcular la optimidad de la aproximación.
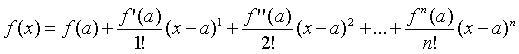
3.- Conceptos Básicos
3.1.- Algoritmo
Un algoritmo es un conjunto de operaciones y procedimientos que deben seguirse para resolver un problema.
El lenguaje algorítmico es aquel por medio del cual se realiza un análisis previo del problema a resolver y encontrar un método que permita resolverlo. El conjunto de todas las operaciones a realizar y el orden en que se deben efectuar, se le denomina algoritmo.
Los pasos para la resolución de un problema son:
Diseño del algoritmo, que describe la secuencia ordenada de pasos que conducen a la solución de un problema dado. (Análisis del problema y desarrollo del algoritmo).
Expresar el algoritmo como un programa de lenguaje de programación adecuado. (Fase de codificación.)
3.2.- Aproximaciones
La mayor parte de las técnicas tiene la característica de poseer errores. Aunque la perfección es una meta digna de alabarse, es difícil, si no imposible, alcanzarla. Sin embargo, sus distribuciones aleatorias se agrupan muy próximas alrededor de la predicción.
En algunos conceptos básicos de los Métodos Numéricos podemos encontrar los siguientes: cifra significativa, precisión, exactitud, incertidumbre y sesgo, que forman parte de las aproximaciones y predicciones numéricas adecuadas.
1.- Los métodos numéricos obtienen resultados aproximados. Por lo tanto, se debe desarrollar criterios para especificar qué tan precisos son los resultados obtenidos.
2.- Aunque ciertos números representan número específicos, no se pueden expresar exactamente con un número finito de cifras. Por lo que podemos tener un algoritmo de aproximación.
4.- Tipos de Errores
4.1.- Error Absoluto
Es la diferencia entre el valor de la medida y el valor tomado como exacto.
Tenemos una recta de 0.613 cm y al medir tenemos una aproximación de 0.6.
Error Exacto = Error Exacto - Error Calculado
4.2.- Error Relativo
Es el cociente entre el error absoluto y el valor exacto. Si se multiplica por 100 se obtiene el tanto % de error.
Una piscina con capacidad de 719 m3, tiene un error absoluto menor a medio metro cúbico, (error < 0,5 m3). Entonces el error relativo (0,5/719) es de 6,954 .
Error Relativo = Error Exacto - Error Calculado / Error Exacto
4.3.- Error Porcentual
Es el resultado de multiplicar el error relativo por 100.
El resultado del error relativo es 6,954. Entonces, el error porcentual es 0,0695.
Error Porcentual = Error relativo x 100
4.4.- Error de Redondeo
Se eliminan cifras significativas de un número a partir de su representación decimal, para obtener un valor aproximado.
5,2536 (a cm) = 5,253 (3 como es <5) = 5,25.
4.5.- Error de Truncamiento
Se refiere al error presente cuando se usa una suma truncada o finita para aproximar la suma de una serie infinita.
Dado el número real 3,1415926, consideramos los 4 dígitos a la derecha de la coma decimal. El resultado es: 3.1415.
Se utiliza la serie infinita de Taylor.
5.- Convergencia
Se entiende por convergencia de un método numérico la garantía de que, al realizar un “buen número” de iteraciones, las aproximaciones obtenidas terminan por acercarse cada vez más al verdadero valor buscado.
En la medida en la que un método numérico requiera de un menor número de iteraciones que otro, para acercarse al valor deseado, se dice que tiene una mayor rapidez de convergencia.
6.- Programas computacionales
Algunos software de computo numéricos son:
Netlib: es una colección grande de software, documentos, bases de datos gratis que son de interés para las comunidades científicas y de métodos numéricos. Netlib contiene software de alta calidad que ha sido probado en forma intensiva, pero todo el software libre no tiene garantía y poco (si existe) soporte. Para poder usar el software, primero se tiene que descargar en su computadora y entonces compilarlo.
Paquetes de software comercial para cómputo numérico general:
NAG: El Grupo de Algoritmos numéricos (NAG) ha desarrollado una biblioteca de Fortran conteniendo alrededor de 1000 subrutinas accesibles al usuario para resolver problemas generales de matemáticas aplicadas, incluyendo: ecuaciones diferenciales ordinarias y parciales, transformada rápida de Fourier, cuadratura, álgebra lineal, ecuaciones no lineales, ecuaciones integrales, y más.
IMSL: La biblioteca numérica de Fortran IMSL hecha por Visual Numerics, Inc. cubre muchas de las áreas contenidas en la biblioteca NAG. También tiene soporte para analizar y presentar datos estadísticos en aplicaciones científicas y de negocios.
NUMERICAL RECIPES: son muy populares entre los ingenieros porque pueden ser usados como libro de cocina donde se puede encontrar una “receta” para resolver algún problema a mano. Sin embargo, el software correspondiente de Numerical Récipes no es comparable en alcance o calidad al dado por NAG o IMSL. Es un software muy usado en universidades, centros de investigación y por ingenieros. En los últimos años ha incluido muchas más capacidades, como la de programar directamente procesadores digitales de señal, crear código VHDL y otras.
MATLAB: Es un programa de cálculo numérico, orientado a matrices y vectores. Por tanto desde el principio hay que pensar que todo lo que se pretenda hacer con él, será mucho más rápido y efectivo si se piensa en términos de matrices y vectores. es un entorno de lenguaje de alto nivel e interactivo que le permite realizar tareas de cálculo más rápidamente que con lenguajes de programación tradicionales, tales como C, C + + y Fortran.
Puede usar MATLAB en una amplia gama de aplicaciones, incluyendo procesamiento de señales e imágenes, comunicaciones, diseño de control, prueba y medición, modelado y análisis financiero y biología computacional. Add-on toolboxes (colecciones de funciones especiales MATLAB) ampliar el entorno de MATLAB para resolver clases particulares de problemas en estas áreas de aplicación.
Características principales
- Lenguaje de alto nivel para la computación técnica
- Entorno de desarrollo para la gestión de código, archivos y datos
- Herramientas interactivas para la exploración iterativa, el diseño y la resolución de problemas
- Funciones matemáticas para álgebra lineal, estadística, análisis de Fourier, filtrado, optimización e integración numérica
- 2-D y 3-D las funciones de gráficos para la visualización de datos
- Herramientas para la creación de interfaces gráficas de usuario
- Funciones para la integración de algoritmos de MATLAB base con aplicaciones externas y lenguajes, como C, C + +, Fortran, Java, COM y Microsoft Excel
GNU OCTAVE: Es un programa libre para realizar cálculos numéricos. Como indica su nombre es parte de proyecto GNU. MATLAB es considerado su equivalente comercial. Entre varias características que comparten se puede destacar que ambos ofrecen un intérprete permitiendo ejecutar órdenes en modo interactivo. Nótese que Octave no es un sistema de álgebra computacional como podría ser GNU Máxima, sino que usa un lenguaje que está orientado al análisis numérico.
7.- Conclusión
Con la ayuda de la computadora y la tecnología podemos realizar los pasos para resolver algún problema, gracias a los métodos numéricos, mediante programas de acceso libre, o si se tiene la suficiente habilidad para generar el programa mismo, se puede hacer.
Hoy en día se cuentan con bastantes programas para la resolución de problemas, tales como algunos mencionados en el punto anterior.
Bibliografia
https://metodosnumericosisc.wordpress.com/2014/09/10/tipos-de-errores/
https://es.slideshare.net/EmmanuelMagaaAquino/12-aproximacion-numerica
https://sites.google.com/site/metnumvmc/unidad-i-2/1-2-1-2-conceptos-basicos-cifra-significativa-precision-exactitud-incertidumbre-y-sesgo
https://sites.google.com/site/metnum00/home/unidad-i/1-1-algoritmos-y-aproximaciones
https://sites.google.com/site/danaly7/unidad-1/1-4-software-de-computo-numerico
