Competencia 5

Ecuaciones Diferenciales Ordinarias

Índice

Ecuaciones diferenciales ordinarias
Método de Euler
Método de Taylor
Métodos de Runge-Kutta

Ecuaciones diferenciales ordinarias.

Un ejemplo de ecuación diferencial ordinaria es: 

Llamaremos ecuacion diferencial ordinaria (abreviado EDO) a una ecuación que involucra a una variable independiente x, una función y(x) y una o varias derivadas de y(x).

Dada una función y = f(x) vamos a estudiar ecuaciones donde aparecen mezcladas la variable x, la función "y" y algunas de sus derivadas y'(x), y''(x)...

El orden de una ecuación diferencial está dado por el orden mayor de su derivada.

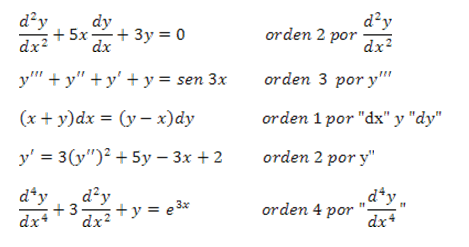
Método de Euler

El Método de Euler o de las Tangentes constituye el primer y más sencillo ejemplo de método numérico para la resolución de un problema de valor inicial: y' = f(x, y), y(x') = y' donde suponemos además que se verifican las hipótesis del Teorema de Picard , y en consecuencia existe solución única para el problema. Interpretando la e.d.o. y' = f(x, y) como un campo de direcciones en el plano x − y y la condición inicial y(x') = y' como un punto (x', y') de dicho plano, podemos aproximar la función solución y(x) por medio de la recta tangente a la misma que pasa por ese punto: 

y(x) ∼= y₀ + f(y₀, y₀)(x − x₀)

donde se ha utilizado que la pendiente de dicha tangente es: m = y₀ (x₀) y, en consecuencia: m = f(x₀, y₀).
Calculamos así de manera aproximada el valor de la solución y en el punto de abscisa x₁ como:
y(x₁) ∼= y₁  = y₀ + f(x₀, y₀)(x₁ − x₀)
y con este punto (aproximado) ya calculado, podemos repetir el m´etodo para obtener otro punto aproximado (x₂, y₂) de la forma: y(x₂) ∼= y₂ = y1 + f(x1, y1)(x₂ − x1) y así sucesivamente.

Es habitual en este método tomar abscisas equiespaciadas, es decir, calcular la solución aproximada en puntos de la forma: xn = xn-1 + h = x0 + nh, siendo h el paso del método. De esta forma se obtienen las fórmulas que nos determinan la solución aproximada en la forma: 
xn = xn-1 + h; yn = yn-1 + f(xn-1, yn-1) h

Desde el punto de vista geométrico, tenemos en definitiva que el Método de Euler aproxima a la función solución por medio de una línea poligonal, la aproximación será tanto peor cuanto mayor sea en número de pasos, es decir, cuanto más “lejos” nos encontremos del punto inicial (x₀, y₀). Por otro lado, el error será evidentemente tanto mayor cuanto más grande sea el “paso” del método, h.



Método de Taylor

El Método de Euler que acabamos de describir no es más que un caso particular de los métodos de Taylor, que consisten de manera general en aproximar la solución por su polinomio de Taylor de un orden determinado. Partiendo por tanto del P.V.I.:
y' = f(x, y)
y(x₀) = y₀ )
tal que presenta solución única y(x) en un entorno de x₀ (solución que suponemos además derivable n veces en dicho entorno), aproximaremos dicha función por su polinomio de Taylor de orden N:

y(x)=y(x₀)+y'(x₀)(x−x₀)+ 1/2 y''(x₀)(x−x₀) 2+ 1/3!y'''(x₀)(x−x₀) 3+. . .+ y^(N)/N! (x−x₀)N

y el error de aproximación viene determinado por el resto de orden N + 1, de manera que el error es proporcional a (x – x₀)^N+1. Si fijamos una sucesión de puntos equiespaciados : x₀, x₁, x₂, . . ., con x_n+1= x_n + h, y denominamos (de manera similar a lo hecho en la sección anterior) y₀, y₁, . . . a los valores aproximados correspondientes de y(x), tendremos que:

Y_n+1= y_n + y’ (x_n)h + (1/2 )y’’(x_n)h² + . . . + (1/N! y)^(N) (xn)h^N

con un error en cada paso proporcional a h^N+1. Para poder aplicar el método necesitamos conocer las derivadas de la solución (recordemos que desconocida), pero teniendo en cuenta la propia ecuación diferencial: y ‘(x_n) = f(x_n, y_n)

mientras que y’’(x_n) puede ser calculada derivando:

y’’= d/dxf(x, y) = ∂f/∂x + ∂f/∂y dy/dx = ∂f ∂x + ∂f/∂y f(x, y) y así sucesivamente.

Es evidente que el método de Taylor de orden uno no es más que el Método de Euler antes descrito.

Métodos de Runge-Kutta

La idea general de los Métodos de Runge-Kutta es sustituir el Problema de Valor Inicial: 
y'=f(x,y)
y=(x0)=y0
por la ecuación integral equivalente: 

para proceder a aproximar esta ´ultima integral mediante un m´etodo num´erico adecuado (recordemos que y(x) es desconocida). Si nuevamente planteamos el problema “paso a paso” tendremos: