Competencia 3

Competencia 3

Índice

Introducción

Sistemas de ecuaciones lineales:

Matriz

Vectores.

Eliminación de Gauss

Regla de Cramer

Descomposición: LU

Gauss-Seidel

INTRODUCCIÓN

Los métodos numéricos son procedimientos por los cuales se obtiene en su mayoría de manera aproximada la solución de ciertos problemas realizando cálculos que son aritméticos y también en su mayoría lógicos (operaciones de aritméticas que son elementales, cálculos de funciones, en consulta de tablas de valores, cálculos preposicionales.

Algún procedimiento consiste en una fila que es finita de procedimientos e instrucciones que son precisas y especifican una secuencia de operaciones algebraicas y lógicas, que producen o bien hacen una aproximación de la solución del problema. La eficiencia del cálculo del cálculo de la aproximación depende, en parte, a la facilidad que se tenga el implementar el algoritmo y de las características especiales y las limitaciones de los instrumentos que son de cálculo.

El análisis numérico trata de diseñar métodos para “aproximar” de una manera eficiente las soluciones de problemas expresados matemáticamente.

Los métodos numéricos son números que los seres humanos han ido construyendo a través del tiempo para superar las diferentes barreras naturales con las que se han encontrado y poder así hacer uso de los mismos con la finalidad de aplicar las Matemáticas a situaciones del mundo real, nos encontramos a menudo con problemas que no pueden ser resueltos analíticamente o de manera exacta y cuya solución debe ser abordada con ayuda de algún procedimiento numérico.

Sistema de ecuaciones lineales.

Se llama sistemas de ecuaciones lineales a un conjunto de “m” ecuaciones lineales en las mismas “n” incógnitas como:

Los métodos de igualación, sustitución o grafico consisten en encontrar y resolver, para cada una de las incognitas, una ecuación con esa incógnita y con ninguna otra ( convirtiendo así un problema difícil en uno mas fácil, a estas ecuaciones, con solo una incógnita, se llega a través de una serie de pasos en los que las ecuaciones intermedias que se van obteniendo tienen menos incognitas que las ecuaciones previas.  Así, es posible que en uno de estos pasos de eliminación de incognitas se utiliza un método ( el de reducción, por ejemplo ) y que, en el siguiente paso, se utiliza otro método ( el de igualación, por ejemplo ). Cada vez que se encuentra la solución para una incógnita, se sustituye esta incógnita por su solución para obtener asi ecuaciones con menos incognitas. 

Así dicha clasificación queda como:

• sistema incompatible




sistema compatible: determinado e indeterminado

Los métodos de igualación, sustitución, reducción y Gauss se pueden utilizar para resolver sistemas de ecuaciones compatibles, ya sean determinados o indeterminados.

Estos mismos métodos también pueden utilizarse para comprobar si un sistema de ecuaciones es compatible o no. La utilización de cualquiera de ellos conduciría, en el caso de que el sistema fuese incompatible, a una igualdad que es falsa, por ejemplo: el método de la matriz inversa y  el de Cramer solo se pueden utilizar en el caso de que el sistema de ecuaciones lineales sea compatible determinado.

Resolución de sistemas de ecuaciones lineales

Resolver un sistema es encontrar todas sus soluciones o decidir que no tiene ninguna.

Para sumar dos matrices A Y B han de ser de las mismas dimensiones; si esto es cierto, la suma es una matriz E de iguales dimensiones que A y que B, y sus elementos se obtienen sumando los elementos correspondientes de A y B.

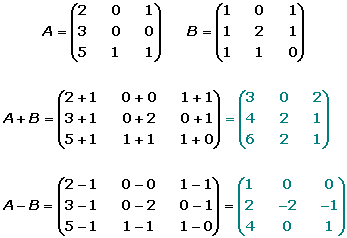
Estas matrices se pudieron sumar porque, ambas son del mismo tamaño.

Multiplicación de matrices

El resultado de multiplicar dos matrices es otra matriz en la que el elemento que ocupa el lugar  cij  se obtiene sumando los productos parciales que se obtienen al multiplicar todos los elementos de la fila “i” de la primera matriz por los elementos de la columna “j” de la segunda matriz. Es decir, multiplicamos la primera fila por los elementos de la primera columna y el resultado será nuestro nuevo elemento. Para ello, el número de columnas de la primera matriz debe coincidir con el de filas de la segunda. Si no fuese así no podríamos realizar la operación.

Matriz por escalar.

Producto de matrices por un escalar

Así como se ha definido la suma de matrices, también se puede formar el producto de un número real A y una matriz A, el resultado, denotado por A es la matriz cuyos elementos son los componentes de A multiplicados por A.

Vectores

Suma de vectores: Para sumar vectores gráficamente dos vectores solemos utilizar la llamada regla del paralelogramo que consiste en trazar por el extremo de cada vector una paralela al otro. 

Analíticamente: se suman las componentes.

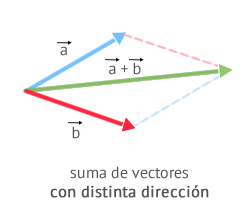
Ejemplo:

Producto de Vectores

El producto escalar de dos vectores no es otro vector sino un número. Se determina multiplicando las coordenadas de ambos vectores, componente a componente y sumando los resultados.

 Eliminación de Gauss.

Resolver un sistema es encontrar todas sus soluciones o decidir que no tiene ninguna.

Un sistema equivalente y escalonado, mediante transformaciones adecuadas.

Se pueden dar los siguientes pasos:

I.             Si es necesario reordenar ecuaciones para que a11 sea distinto de cero.

II.     Dividir la primera ecuación por a11 y restar a cada ecuación un múltiplo de la primera para eliminar todos los elementos que quedan por debajo de a11x1.

III.          Repetir los pasos anteriores basados ahora en a22 (y si es necesario en cada aii).

IV.          El proceso termina cuando no quedan más ecuaciones.

Eliminación Gauss-Jordan

En matemáticas, la eliminación de Gauss, llamada así debido a Carl Friedrich Gauss y Wilhelm Jordan, es un algoritmo del álgebra lineal para determinar las soluciones de un sistema de ecuaciones lineales, encontrar matrices e inversas. Un sistema de ecuaciones se resuelve por el método de Gauss cuando se obtienen sus soluciones mediante la reducción del sistema dado a otro equivalente en el que cada ecuación tiene una incógnita menos que la anterior. El método de Gauss transforma la matriz de coeficientes en una matriz triangular superior. El método de Gauss-Jordan continúa el proceso de transformación hasta obtener una matriz diagonal.

1. Ir a la columna no cero extrema izquierda
2. Si la primera fila tiene un cero en esta columna, intercambiarlo con otra que no lo tenga.
3. Luego, obtener ceros debajo de este elemento delantero, sumando múltiplos adecuados del renglón superior a los renglones debajo de él.
4. Cubrir el renglón superior y repetir el proceso anterior con la submatriz restante. Repetir con el resto de los renglones (en este punto la matriz se encuentra en forma escalonada).
5. Comenzando con el último renglón no cero, avanzar hacia arriba: para cada renglón obtener 1 delantero e introducir ceros arriba de éste sumando múltiplos correspondientes a los renglones correspondientes.

Una variante interesante de la eliminación de Gauss es la que llamamos eliminación de Gauss-Jordan, (debido al mencionado Gauss y a Wilhelm Jordan), esta consiste en ir obteniendo los 1 delanteros durante los pasos uno al cuatro (llamados paso directo) así para cuando estos finalicen ya se obtendrá la matriz en forma escalonada reducida.

Regla de Cramer

Esta regla establece que cada incógnita de un sistema de ecuaciones lineales algebraicas puede expresarse como una fracción de dos determinantes con denominador d y con el numerador obtenido a partir de d, al reemplazar la columna de coeficientes de la incógnita en cuestión por las constantes b₁, …b₂,…, b_n. por ejemplo, x₁ se calcula como:

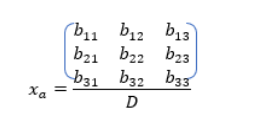
La regla de Cramer da una solución para sistemas compatibles determinados en términos de determinantes y adjuntos dada por:

Donde Aj es la matriz resultante de remplazar la j-ésima columna de A por el vector columna b. Para un sistema de dos ecuaciones y dos incógnitas:

La regla de Cramer da la siguiente solución:

Descomposición LU.

Para encontrar la matriz triangular inferior se busca hacer ceros los valores de arriba de cada pivote, así como también convertir en 1 cada pivote. Se utiliza el mismo concepto de "factor" explicado anteriormente y se ubican todos los "factores" debajo de la diagonal según corresponda en cada uno.

Esquemáticamente se busca lo siguiente:

  

Originalmente se tenía:

Debido a que [A] = [L][U], al encontrar [L] y [U] a partir de [A] no se altera en nada la ecuación y se tiene lo siguiente:

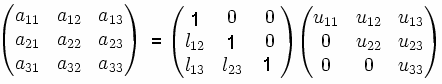
Por lo tanto, si Ax = b, entonces LUx = b, de manera que Ax = LUx = b.

Descomposición Gauss-Seidel

Pasos de resolución método Gauss-Seidel

1. Obtener la matriz triangular inferior L y la matriz triangular superior U.
2. Resolver Ly = b (para encontrar y).
3. El resultado del paso anterior se guarda en una matriz nueva de nombre "y".
4. Realizar Ux = y (para encontrar x).
5. El resultado del paso anterior se almacena en una matriz nueva llamada "x", la cual brinda los valores correspondientes a las incógnitas de la ecuación.